http://davidakenny.net/cm/mediate.htm 에서 발췌
----------------------------------------------
What Is Mediation?
Consider a variable X that is assumed to affect another variable Y. The variable X is called the initial variable and the variable that it causes or Y is called the outcome. In diagrammatic form, the unmediated model is

The effect of X on Y may be mediated by a process or mediating variable M, and the variable X may still affect Y. Path c is called the total effect. The mediated model is
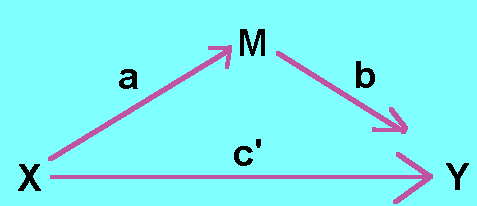
(These two diagrams are essential to the understanding of this page. Please study them carefully!) Path c' is called the direct effect. The mediator has been called an intervening or process variable. Complete mediation is the case in which variable X no longer affects Y after M has been controlled and so path c' is zero. Partial mediation is the case in which the path from X to Y is reduced in absolute size but is still different from zero when the mediator is controlled.
Note that a mediational model is a causal model. For example, the mediator is presumed to cause the outcome and not vice versa. If the presumed model is not correct, the results from the mediational analysis are of little value. Mediation is not defined statistically; rather statistics can be used to evaluate a presumed mediational model. The reader should consult the section below on Specification Error.
There is a long history in the study of mediation (Hyman, 1955; MacCorquodale & Meehl, 1948). Currently mediation is a very popular topic. (This page averages over 100 different visitors a day.) There are several reasons for the intense interest in this topic. One reason for testing mediation is trying to understand the mechanism through which the initial variable affects the outcome. Mediation (and moderation) analysis are a key part of what has been called process analysis. Moreover when most causal or structural models are examined, the mediational part of the model is the most interesting.
Baron and Kenny Steps If the mediational model (see above) is correctly specified, the paths (c, a, b, and c') can be estimated by multiple regression, sometimes call ordinary least squares or OLS. As discussed later, other methods of estimation (e.g., logistic regression and structural equal modeling) can be used. Regardless of which data analytic method (the general assumption on this page is that the method is multiple regression) is used, the steps necessary for testing mediation are the same. This section describes the analyses required for testing mediational hypotheses [previously presented by Baron and Kenny (1986) and Judd and Kenny (1981)].
Baron and Kenny (1986) and Judd and Kenny (1981) have discussed four steps in establishing mediation:
If all four of these steps are met, then the data are consistent with the hypothesis that variable M completely mediates the X-Y relationship, and if the first three steps are met but the Step 4 is not, then partial mediation is indicated. Meeting these steps does not, however, conclusively establish that mediation has occurred because there are other (perhaps less plausible) models that are consistent with the data. Some of these models are considered later in the Specification Error section. Note that the steps are stated in terms of zero and nonzero coefficients, not in terms of statistical significance, as they were in Baron and Kenny (1986). Because trivially small coefficients can be statistically significant with large sample sizes and very large coefficients can be nonsignificant with small sample sizes, the steps should not be defined in terms of statistical significance. Statistical significance is informative, but other information should be part of statistical decision making. For instance, consider the case in which a is large, b is zero, and so c = c'. It is very possible that the statistical test of c' is not significant (due to the collinearity of X and M) whereas c is significant. It would then appear that there is complete mediation when if fact there is no mediation at all.
Following, Kenny, Kashy, and Bolger (1998), one might ask whether all of the steps have to be met for there to be mediation. Certainly, Step 4 does not have to be met unless the expectation is for complete mediation. In the opinion of most though not all analysts, Step 1 is not required. However, note that a path from the initial variable to the outcome is implied if Steps 2 and 3 are met. If c' were opposite in sign to ab something that MacKinnon, Fairchild, and Fritz (2007) refer to as "inconsistent mediation," then it could be the case that Step 1 would not be met, but there is still mediation. In this case the mediator acts like a suppressor variable. Most analysts believe that the essential steps in establishing mediation are Steps 2 and 3.
James and Brett (1984) have argued that Step 3 should be modified by not controlling for the initial variable. Their rationale is that if there is complete mediation, there would be no need to control for the initial variable. However, because complete mediation does not always occur, it would seem sensible to control for X in Step 3.
Measuring Mediation or the Indirect Effect The amount of mediation, which is called the indirect effect, is defined as the reduction of the effect of the initial variable on the outcome or c - c'. This difference in coefficients is theoretically exactly the same as the product of the effect of X on M times the effect of M on Y or ab; thus it holds that ab ≈ c - c'. The two are exactly equal when a) multiple regression (or structural equation modeling without latent variables) is used, b) there are no missing data, c) and the same covariates are in the equation. However, the two are only approximately equal for multilevel models, logistic analysis and structural equation model with latent variables. For such models, it is probably inadvisable to compute c from Step 1, but rather c (sometimes called the total effect, should be inferred to be c' + ab and not directly computed. Note that the amount of reduction in the effect of X on Y is not equivalent to either the change in variance explained or the change in an inferential statistic such as F or a p value. It is possible for the F from the initial variable to the outcome to decrease dramatically even when the mediator has no effect on the outcome! It is also not equivalent to a change in partial correlations.
If Step 2 (the test of a) and Step 3 (the test of b) are met, it follows that there necessarily is a reduction in the effect of X on Y. One way to test the null hypothesis that ab = 0 is to test that both a and b are zero (Steps 2 and 3). If such a strategy were used and one wanted a .05 probability of the combined test that a = 0 and b = 0, then alpha for the tests of a and b should lowered to .0253 so that the Type I error protection rate is correct.
It is much more common and more highly recommended (MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002) to perform a single test of ab is used . The test was first proposed by Sobel (1982). It requires the standard error of a or sa (which equals a/ta where ta is the t test of coefficient a) and the standard error of b or sb. The Sobel test provides the standard error of ab can be shown to equal approximately the square root of
Other standard errors have been proposed, but the Sobel test has been by far the most commonly reported. (Though see below as bootstrapping seems to be replacing the more conservative Sobel test.) The test of the indirect effect is given by dividing ab by the square root of the above variance and treating the ratio as a Z test (i.e., larger than 1.96 in absolute value is significant at the .05 level). Kristopher J. Preacher and Geoffrey J. Leonardelli have an excellent web page that can help you calculate these test (go to the Sobel test). Measures and tests of indirect effects are also available within many structural equation modeling programs. These programs appear to use the Sobel formula.
The derivation of the Sobel standard error presumes that a and b are independent, something that is true when the tests are from multiple regression but not true when other tests are used (e.g., logistic regression, structural equation modeling, and multilevel modeling). In such cases, the researcher ideally provides evidence for approximate independence. Additionally, the Sobel test can be conducted using the standardized or unstandardized coefficients. Care must be taken to use the appropriate standard errors if standardized coefficients are used.
The Sobel test is very conservative (MacKinnon, Warsi, & Dwyer, 1995), An increasingly popular alternative is bootstrapping (Shrout & Bolger, 2002) which is beginning to replace the Sobel test of the indirect effect. Hayes and Preacher have written SPSS and SAS macros that can be downloaded for tests of indirect effects (click here to go Kris Preacher's page). Also Amos can be used to bootstrap (click here for a tutorial).
A related measure of mediation is the proportion of the effect that is mediated or 1 - ab/c. Such a measure while theoretically informative is very unstable and should not be computed is c is small. Note too that it is greater than 1 when there is inconsistent mediation. The measure can be informative, especially when c' is not statistically significant. See the example in Kenny et al. (1998) where c' is not statistically significant but only 56% of c is explained.
Design Issues Distal and Proximal Mediation To demonstrate mediation both paths a and b need to be relatively large. Generally, the maximum size of the product ab is c, and so as path a increases, path b must decrease and vice versa.
The mediator can be too close in time or in the process to the initial variable and so path a would be relatively large and path b relatively small. An example of a proximal mediator is a manipulation check. The use of a very proximal mediator creates multicollinearity which is discussed in the next section.
Alternatively, the mediator can be chosen too close to the outcome and with a distal mediator path b is large and path a is small. Ideally in terms of power, standardized a and b should be comparable in size. Work by Hoyle and Kenny (1999) shows that the power of the test of ab is maximal when b is somewhat larger than a. So distal mediators result in somewhat greater power than proximal mediators.
Multicollinearity
If M is a successful mediator, it is necessarily correlated with X due to path a. This correlation, called collinearity, affects the precision of the estimates of the last set of regression equations. If X were to explain all of the variance in M, then there would be no unique variance in M to explain Y. Given that a is nonzero, the power of the tests of the coefficients b and c' is compromised. The effective sample size for these tests is approximately N(1 - r2) where N is the total sample size and r is the correlation between the initial variable and the mediator. So if M is a strong mediator (path a is large), to achieve equivalent power the sample size would have to be larger than what it would be if M were a weak mediator. Thus, multicollinearity is to be expected in a mediational analysis and it cannot be avoided.
Specification Error Mediation is a hypothesis about a causal network. (See Kraemer, Wilson, Fairburn, and Agras (2002) who attempt to define mediation without making causal assumptions.) The conclusions from a mediation analysis are valid only if the causal assumptions are valid. In this section, the three major assumptions of mediation are discussed. Mediation analysis makes all of the standard assumptions of the general linear model (i.e., linearity, normality, homogeneity of error variance, and independence of errors).
Reverse Causal Effects
The mediator may be caused by the outcome variable (Y would cause M in the above diagram). When the initial variable is a manipulated variable, it cannot be caused by either the mediator or the outcome. But because both the mediator and the outcome variables are not manipulated variables, they may cause each other.
Often it is advisable to interchange the mediator and the outcome variable and have the outcome "cause" the mediator. If the results look similar to the specified mediational pattern (i.e., the c' and b are about the same in the two models), one would be less confident in the specified model.
Sometimes reverse causal effects can be ruled out theoretically. That is, a causal effect in one direction does not make sense. Design considerations may also weaken the plausibility of reverse causation. Ideally, the mediator should be measured temporally before the outcome variable.
If it can be assumed that c' is zero, then reverse causal effects can be estimated. That is, if it can be assumed that there is complete mediation (X does not directly cause Y and so c' is zero), the mediator may cause the outcome and the outcome may cause the mediator.
Smith (1982) has developed another method for the estimation of reverse causal effects. Both the mediator and the outcome variables are treated as outcome variables, and they each may mediate the effect of the other. To be able to employ the Smith approach, for both the mediator and the outcome, there must be a different variable that is known to cause each of them but not the other. So a variable must be found that is known to cause the mediator but not the outcome and another variable that is known to cause the outcome but not the mediator. These variables are called instrumental variables. Thus, mediation can be estimated and tested with models of feedback.
Measurement Error in the Mediator
If the mediator is measured with less than perfect reliability, then the effects (b and c') are likely biased. The effect of the mediator on the outcome (path b) is likely underestimated and the effect of the initial variable on the outcome (path c') is likely over-estimated if ab is positive (which is typical). The over-estimation of c' is exacerbated to the extent to which path a is large.
To remove the biasing effect of measurement error, multiple indicators of the mediator can be used to tap a latent variable. Alternatively, instrumental variable estimation can be used, but as before, it must be assumed that c' is zero. Also possible is to fix the error variance at the value or one minus the reliability quantity times the variance of the measure. If none of these approaches is used, the researcher needs to demonstrate that the reliability of the mediator is very high so that the bias is fairly minimal.
Omitted Variables
In this case, there is a variable that causes both variables in the equation. For example, at Step 3, there is a variable that causes both the mediator and the outcome. This is the most difficult specification error to solve and unfortunately this key assumption is not directly discussed in Baron and Kenny (1986). (It is discussed in Judd and Kenny (1981).) Although there has been some work on the omitted variable problem, the only complete solution is to specify and measure such variables and control for their effects. Note that if the initial variable is randomized, then omitted variables do not bias the estimates at Steps 1 and 2. Even, if X is manipulated, path c' is biased is there is an omitted variable that causes M and Y.
Sometimes the source of correlation between the mediator and the outcome is a common method effect. For instance, the measuring scale of the two variables is the same. Ideally, efforts should be made to ensure that the two variables do not share method effects (e.g., both are self-reports from the same person). A latent variable analysis might be used to remove the effects of correlated measurement error.
Extensions Mediated Moderation and Moderated Mediation
Moderation means that the effect of a variable on an outcome is altered (i.e., moderated) by another variable. Moderation is usually captured by an interaction of two initial variables. If this moderation is mediated, then we have the usual pattern of mediation but the X variable is an interaction and is referred to as mediated moderation. (To read about moderation click here.) All the Baron and Kenny steps would be repeated with the effect of Step 1 being an interaction, and the two main effects would be treated as "covariates."
A variable may act as a mediator stronger for one group (e.g., males) than for another (e.g., females). There are two different forms of moderated mediation. The effect of the initial variable on the mediator may differ as a function of the moderator (i.e., path a varies) or the mediator may interact with the moderator to cause the outcome (i.e., path b varies). Note that interactions are commonly testing by computing a product term, but there are other ways to specify the interaction (e.g., absolute difference). Theory should inform the proper specification of the interaction.
Papers by Muller, Judd, and Yzerbyt (2005) and Edwards and Lambert (2007) discuss the relationship between mediated moderation and moderated mediation. They also present examples of each.
Multiple Mediators or Outcomes
If there are multiple mediators, they can be tested simultaneously or separately. The advantage of doing them simultaneously is that one learns if the mediation is independent of the effect of the other mediators. One should make sure that the different mediators are conceptually distinct and not too highly correlated. (Kenny, Kashy, and Bolger (1998) consider an example with two mediators.) There is an interesting case of two mediators in which ab is opposite sign. The sum of indirect effects would be near zero. It might then be possible that c is near zero, because there are two indirect effects that work in the opposite direction. In this case "no effect" would be mediated.
If there are multiple outcomes, they can be tested simultaneously or separately. If tested simultaneously, the entire model can be estimated by structural equation modeling.
Latent Variables
In this case the analysis would be done by a structural equation modeling program (e.g., LISREL, Amos, Eqs, or MPlus). Some programs provide measures and tests of indirect effects. Also such programs are quite flexible in handling multiple mediators and outcomes. The one complication is how to handle Step 1. That is, if two models are estimated, one with the mediator and one without, the paths c and c' are not comparable because the factor loadings would be different. It is then inadvisable to test the relative fit of two structural models, one with the mediator and one without. Rather c, the total effect, can be estimated using the formula of c' + ab.
Covariates
There are often variables that do not change that can cause or be correlated with the initial variable, mediator, and outcome (e.g., age, gender, and ethnicity); these variables are commonly called covariates. They would generally be included in each equation and would not be trimmed from equations unless they are dropped from all of the equations.
Dichotomous Variables
In this case either the mediator or the outcome is a dichotomy. Having the initial variable be a dichotomy is not problematic. In this case the analysis would likely be conducted using logistic regression when the criterion measure is dichotomous. One can still use the Baron and Kenny steps and the Sobel test. The one complication is the computation of indirect effect the degree of mediation, but coefficients need to be transformed. (To read about the computation of indirect effects click here.)
Multilevel Modeling
Estimation of mediation within multilevel models can be very complicated, especially when the mediation occurs at level one and when that mediation is allowed to be random, i.e., vary across level two units. The reader is referred to Krull and MacKinnon (1999), Kenny, Korchmaros, and Bolger (2003), and Bauer and Preacher (2006) for a discussion of this topic.
Links to Other Sites The mediation site of Dave MacKinnon. References
To find out why computing partial correlations to test mediation is wrong.
Kris Preacher's papers and programs.
Go to my moderation page.
A paper I have written called "Reflections on Mediation."
Baron, R. M., & Kenny, D. A. (1986). The moderator-mediator variable distinction in social psychological research: Conceptual, strategic and statistical considerations. Journal of Personality and Social Psychology, 51, 1173-1182.
Bauer, D. J., Preacher, K. J., & Gil, K. M. (2006). Conceptualizing and testing random indirect effects and moderated mediation in multilevel models: New procedures and recommendations. Psychological Methods, 11, 142-163.
Edwards, J. R., & Lambert L. S. (2007). Methods for integrating moderation and mediation: A general analytical framework using moderated path analysis. Psychological Methods, 12, 1-22.
Hoyle, R. H., & Kenny, D. A. (1999). Statistical power and tests of mediation. In R. H. Hoyle (Ed.), Statistical strategies for small sample research. Newbury Park: Sage.
Hyman, H. H. (1955). Survey design and analysis. New York: Glencoe, IL: The Free Press.
James, L. R., & Brett, J. M. (1984). Mediators, moderators and tests for mediation. Journal of Applied Psychology, 69, 307-321.
Judd, C. M., & Kenny, D. A. (1981). Process analysis: Estimating mediation in treatment evaluations. Evaluation Review, 5, 602-619.
Kenny, D. A., Kashy, D. A., & Bolger, N. (1998). Data analysis in social psychology. In D. Gilbert, S. Fiske, & G. Lindzey (Eds.), The handbook of social psychology (Vol. 1, 4th ed., pp. 233-265). Boston, MA: McGraw-Hill.
Kenny, D. A., Korchmaros, J. D., & Bolger, N. (2003). Lower level mediation in multilevel models. Psychological Methods, 8, 115-128.
Kraemer H. C., Wilson G. T., Fairburn C. G., & Agras W. S. (2002). Mediators and moderators of treatment effects in randomized clinical trials. Archives of General Psychiatry, 59, 877-883.
Krull, J. L. & MacKinnon, D. P. (1999). Multilevel mediation modeling in group-based intervention studies. Evaluation Review, 23, 418-444.
MacCorquodale, K., & Meehl, P. E. (1948). On a distinction between hypothetical constructs and intervening variables. Psychological Review, 55, 95-107.
MacKinnon, D. P., Fairchild, A. J., & Fritz, M. S. (2007). Mediation analysis. Annual Review of Psychology, 58,, 593-614.
MacKinnon, D. P., Lockwood, C. M., Hoffman, J. M., West, S. G., & Sheets, V. (2002). A comparison of methods to test the significance of the mediated effect. Psychological Methods, 7, 83-104.
MacKinnon, D. P., Warsi, G., & Dwyer, J. H. (1995). A simulation study of mediated effect measures. Multivariate Behavioral Research, 30, 41-62.
Muller, D., Judd, C. M., & Yzerbyt, V. Y. (2005). When moderation is mediated and mediation is moderated. Journal of Personality and Social Psychology, 89,, 852-863.
Shrout, P. E., & Bolger, N. (2002). Mediation in experimental and nonexperimental studies: New procedures and recommendations. Psychological Methods, 7, 422-445.
Smith, E. (1982). Beliefs, attributions, and evaluations: Nonhierarchical models of mediation in social cognition. Journal of Personality and Social Psychology, 43,248-259.
Sobel, M. E. (1982). Asymptotic confidence intervals for indirect effects in structural equation models. In S. Leinhardt (Ed.), Sociological Methodology 1982 (pp. 290-312). Washington DC: American Sociological Association.
'statistics > 구조방정식(AMOS를 중심으로)' 카테고리의 다른 글
| [스크랩] 매개효과(1) (0) | 2009.01.10 |
|---|---|
| 매개된 조절효과, 조절된 매개효과 (0) | 2008.12.07 |
| [스크랩] Online Sobel-test site for mediation effects (0) | 2008.10.31 |
| 매개변인과 조절변인(중재변인)이란? (0) | 2008.10.08 |
| 매개효과를 회귀분석으로 보고자할 때 근거가 되는 논문. (0) | 2008.10.08 |